Minor Key Signatures
The most important first step in learning about minor key signatures is, strangely enough, to learn the major key signatures! As you will see below, once you have learned these, you already know the minor key signatures.
Click here to learn about major key signatures with sharps.
Click here to learn about major key signatures with flats.
Once you know these, carry on.
Minor key signatures
Here is a slightly modified excerpt from my book Essential Music Theory Volume 1: Learn To Read And Appreciate Music.
Each minor scale has a relative major, like a cousin! A relative minor has the same key signature as the major of which it is a relative. To find the relative major of a minor key you go up three semitones. So, beginning on A and moving up three semitones, it is clear that C major is the relative major and this has the same key signature as A minor.
It often helps to visualize this on a piano keyboard. As you can see below, starting on A and going up 3 semitones brings you to C; A minor has the same key signature as C major.
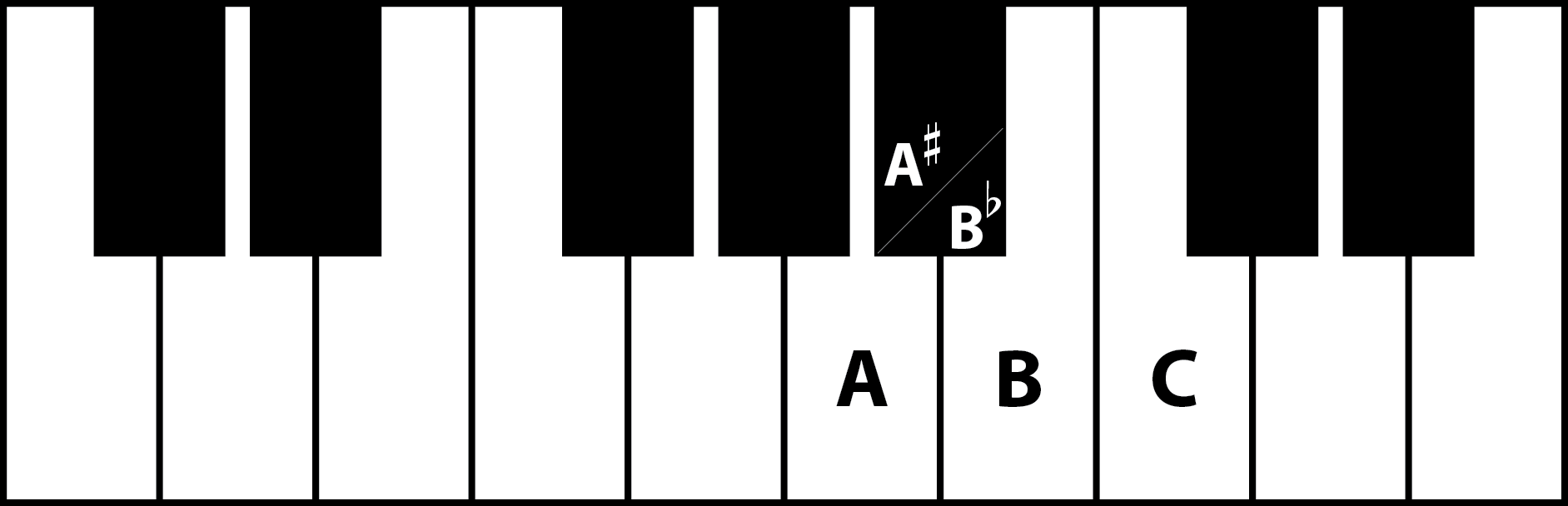
Other examples of relative minors
In the same way the relative major of D minor is F major (one flat), and the relative major of E minor is G major (one sharp).
You can also find the relative major of a minor key by going up three semitones. So it follows that the relative major of B minor is D major, both have two sharps. The relative major of G minor is B♭major, both have two flats.
Of course, you can also find out the relative minor of a particular major scale by going down 3 semitones. E.g., the relative minor of A major is F# minor, the relative minor of Bb major is G minor.
To help you remember this, just remember that a major is high up in the army, so to get to a major you need to go up. It also works the other way, a miner works underground in a mine, so to get to a minor you need to go down.
The importance of the minor 3rd
The one issue that sometimes crops up is deciding which name to call certain notes. For instance, if you are looking for the relative major of G minor and you go up three semitones on a piano keyboard you arrive on the black note at the top of a group of three. This can be called A# or Bb. A# and Bb major have very different key signatures! To help make sure you find the correct note, always remember that the note should be a 3rd above the minor key signature you are trying to find. In this example G - A is a 2nd, but G - B is a 3rd. Therefore we can see that the relative major to G minor is Bb major (2 flats, Bb and Eb).
To read more about minor keys and minor scales click on the link below to go to the iBooks Store and buy my brand new interactive theory book.
Alternatively, if you don't have an Apple device, you can also buy a (non interactive) kindle version from Amazon.
And if you are really stuck and need to know straight away here is an image of all the minor key signatures!
A Clear Path To Learning Music Theory
For more help check out my new theory book Essential Music Theory: Learn To Read And Appreciate Music Vol. 1 available for iPad and Mac OS.
- A simple step-by-step course that takes you from complete beginner to grade 2 music theory
- Multi-faceted learning - audio, video, mind maps, clear musical examples
- Built in quizzes to check your understanding
Click here for more information.
Or get it on the iBooks Store!

